Формула расчета сложных процентов по вкладу — как рассчитать ее самостоятельно
В последнее время банки активно привлекают вклады населения, заманивая вкладчиков высокими декларируемыми в рекламе процентными ставками. Однако по факту может оказаться, что наибольший доход можно получить по вкладу, у которого декларируемая процентная ставка ниже, чем в активно рекламируемом вкладе.
Ранее мы уже писали о том, как выбрать лучший вклад. Сегодня поговорим о том, как правильно посчитать эффективную ставку по вкладу, или сколько процентов годовых вы получите реально за весь срок накоплений.
В самом простом случае, когда ставка по вкладу не меняется в течение всего периода и проценты выплачиваются по окончании срока действия договора, посчитать доход по вкладу просто, и в этом случае эффективная процентная ставка буде в точности равна ставке по договору. Сложнее обстоит ситуация с вкладами, у которых ставка меняется со временем, возможна периодическая капитализация, возможно пополнение и/или частичное снятие.
Формула расчета сложных процентов
Давайте по порядку. Возьмем относительно простой случай, когда проценты начисляются ежемесячно и капитализируются. Другими словами, каждый месяц происходит начисление причитающихся вам процентов и их сумма добавляется к сумме вклада. Соответственно, в следующем месяце проценты будут начисляться и на сам вклад, и на ранее начисленные проценты (то есть проценты на проценты). Продолжая логику рассуждений таким образом не трудно убедиться, что проценты ежемесячно будут нарастать в геометрической прогрессии. А если проценты начисляются и капитализируются ежедневно? Считается такая эффективная доходность по формуле:
Здесь главное – правильно посчитать количество выплат в году. Если условиями привлечения вклада предусмотрена ежемесячная капитализация, то количество выплат в году равно 12, если ежедневная, то 365. Если, например, 50 дней, то количество выплат в году равно 365/50.
Расчет доходности вклада
Чтобы посчитать реальную доходность такого вклада можно воспользоваться стандартной функцией в Excel под названием «ЭФФЕКТ». У нее два параметра: ставка по вкладу (ее надо указывать или со знаком «%» или делить на 100, чтобы посчиталось правильно) и количество выплат по вкладу в году (то, что у нас называется количеством выплат в году).
Если условиями вклада предусмотрено, что ставка со временем изменяется, то тогда считать придется сложнее. Подсчеты рекомендуется перепроверять, так как в подсчетах Excel могут встречаться ошибки. Предлагаемая ниже схема расчетов очень удобна для расчета всех вариантов вклада: с пополнениями, частичными снятиями и другими изменениями на счету. В данном примере приведен порядок изменения условий по вкладу (столбец «Ставка»), срок вклада – 36 месяцев (3 года), капитализация процентов (причисление к сумме вклада) – ежемесячная, то есть 12 раз.
| Количество выплат в год | 12 | |
| Срок, месяцев | 36 | |
| Сумма вклада | 10 000 р. | |
| Ставка | Накопленный остаток | |
| янв.12 | 10% | 10 083р. |
| фев.12 | 10% | 10 167р. |
| мар.12 | 10% | 10 252р. |
| апр.12 | 10% | 10 338р. |
| май.12 | 10% | 10 424р. |
| июн.12 | 10% | 10 511р. |
| июл.12 | 10% | 10 598р. |
| авг.12 | 10% | 10 686р. |
| сен.12 | 10% | 10 775р. |
| окт.12 | 10% | 10 865р. |
| ноя.12 | 10% | 10 956р. |
| дек.12 | 10% | 11 047р. |
| янв.13 | 9% | 11 130р. |
| фев.13 | 9% | 11 213р. |
| мар.13 | 9% | 11 298р. |
| апр.13 | 9% | 11 382р. |
| май.13 | 9% | 11 468р. |
| июн.13 | 9% | 11 554р. |
| июл.13 | 9% | 11 640р. |
| авг.13 | 9% | 11 728р. |
| сен.13 | 9% | 11 816р. |
| окт.13 | 9% | 11 904р. |
| ноя.13 | 9% | 11 993р. |
| дек.13 | 9% | 12 083р. |
| янв.14 | 8% | 12 164р. |
| фев.14 | 8% | 12 245р. |
| мар.14 | 8% | 12 327р. |
| апр.14 | 8% | 12 409р. |
| май.14 | 8% | 12 492р. |
| июн.14 | 8% | 12 575р. |
| июл.14 | 8% | 12 659р. |
| авг.14 | 8% | 12 743р. |
| сен.14 | 8% | 12 828р. |
| окт.14 | 8% | 12 914р. |
| ноя.14 | 8% | 13 000р. |
| дек.14 | 8% | 13 086р. |
Накопленный остаток на каждую дату считается как «остаток в предыдущем месяце» * (1+ «действующая ставка» / «количество периодов выплаты»).
Для первого расчета «остаток в предыдущем месяце» равен первоначальной сумме вклада. Эффективная ставка рассчитывается как конечный остаток (13 086 рублей), поделенный на первоначальную сумму вклада (10 000 рублей), приведенный к процентам годовых (то есть поделенный на 3). Должно получиться 10,29 %.
После модификации эта таблица будет удобна для расчета будущего дохода, если вы планируете пополнять вклад. Для этого нужно добавить в формулу расчета накопленного остатка прибавление суммы пополнения. Другое дело, что эффективную ставку уже нельзя будет считать по приведенной выше схеме, в особенности, если пополнений будет много в течение всего срока действия вклада – в таких условиях действуют другие математические формулы.
Начисление сложных процентов по вкладам и инвестициям
Любой человек в современном мире рано или поздно сталкивается со сложным процентом. Как правило, знакомство со сложными процентами происходит в банке при расчете доходности по вкладу. Поскольку знание этого понятия является фундаментальным для любого инвестора, поэтому решил посвятить этой теме целую статью, в которой раз и навсегда разобраться в начислении сложных процентов. Для удобства я буду рассматривать явление сложных процентов на примере банковских вкладов. Надеюсь, что эта статья будет полезна не только новичкам в инвестировании, но и опытным инвесторам для правильного планирования доходности портфеля.
Итак, что же такое сложный процент. Говоря простым языком, это постоянное увеличение инвестиционного капитала за счет прибыли, при этом полученный доход участвует в получении новой прибыли за следующий расчетный период. Магия сложных процентов заключается в ускоренном росте капитала и прибыли, за счет постоянного реинвестирования, в банках еще это называют капитализацией.
- Как рассчитать сложный процент по вкладу в банке
- Формулы расчета сложных процентов
- Арифметика прибыли
- Вклад со сложным процентом
- Кредит со сложным процентом
- Формула расчета сложных процентов
- Что еще почитать на эту тему?
- Что нужно знать при расчете процентов по вкладам (депозитам)
- Ежемесячные платежи: принцип формирования
- Как посчитать проценты от числа: Высчитать и рассчитать проценты по кредиту — Формула сложных процентов
- Примеры вычислений
- Формула дохода
- Формула простых процентов
- Формула сложных процентов
- Вклады с простым процентом
- Вклады со сложным процентом
- Наращение по простым процентам
- Дисконтирование по сложным процентам
- Изучите простые и сложные проценты в практическом курсе «Финансовый менеджмент: управление финансами» :
- Изучите сегодня
- Контурная/объемная коррекция губ и периоральной области. Лучшие подходы и техники аугментации
- Этикет и навыки делового общения
- Техники скорочтения
- IV Продвинутый диссекционный кадавер-курс по инвазивным методикам коррекции различных зон лица. День третий: мастер-класс живых инъекций
- Валеология
- Конкурентная разведка
- Креативность и интеллект: развитие творческих и аналитических способностей
- Диссекционный кадавер-курс по инъекционным методикам в косметологии. День третий: live-инъекции
- Развитие интуиции и наблюдательности
- Также смотрите
- Как начисляются проценты по вкладам
- Капитализация процентов
- Расчет прибыли для вклада с пополнением
Как рассчитать сложный процент по вкладу в банке

Я веду этот блог уже более 6 лет. Все это время я регулярно публикую отчеты о результатах моих инвестиций. Сейчас публичный инветпортфель составляет более 1 000 000 рублей.
Специально для читателей я разработал Курс ленивого инвестора, в котором пошагово показал, как наладить порядок в личных финансах и эффективно инвестировать свои сбережения в десятки активов. Рекомендую каждому читателю пройти, как минимум, первую неделю обучения (это бесплатно).
Прежде чем понять, как рассчитать сложный процент по вкладу, давайте разберемся с простыми процентами. Простые проценты часто используют при подсчете прибыли по банковскому депозиту, со снятием дохода в расчетные периоды. К примеру, если мы инвестируем 100$ на 10 лет под 10% годовых, то через год мы сможем забрать всего 110$. А после окончания срока депозита, вклад удвоится.
1-й год: 100$ + 100$*0,10 = 110$ 10-й год: 100 + 100$*0,10*10 лет = 200$
Ощутимым преимуществом простых процентов (инвестирования без капитализации), является возможность использование текущей прибыли в других целях.
Теперь на этом же простом примере разберем, как просчитать сложный процент при ежегодной капитализации.
1-й год: 100 + 10% = 110$ 2-й год: 110 + 10% = 121$ 10-й-год: 236 + 10% = 260$
Как видно из примера, сложный банковский процент существенно интереснее, с применением этого метода прибыль вкладчика на 30% больше, чем при простом проценте. Эта сумма может быть еще большей, если применять не ежегодную капитализацию (начисление процентов), а ежеквартальную или ежемесячную.
Суть процесса начисления сложных процентов с капитализацией в том, что доход приносит не только первоначальная сумма вклада, но и каждое начисление прибыли. При этом сумма увеличивается с большой скоростью, и чем чаще будет фиксироваться прибыль, тем больше будет доход.
Формулы расчета сложных процентов
Посчитать сложный процент на любом калькуляторе можно по следующей формуле:
C=C0 *(1+P*m/100*12)^n
C — итог, C0 — сумма первоначального вклада, P — процент годовых, m — период капитализации (месяц), n — периоды инвестирования.
Можно посчитать и сложный процент с пополнением (D), формула для расчета, правда, будет выглядеть немного страшнее ? :
C=C0 *(1+P*m/100*12)^n + (D *(1+P*m/100*12)^(n+1) — D *(1+P*m/100*12)) / (P*m)/100*12)
Эту же формулу расчета сложных процентов можно использовать и для банковских вкладов.
На самом деле формулы нужны только тем, кто хочет досконально разобраться в вопросе. В наш век информационных технологий существует множество инструментов, с помощью которых можно без труда рассчитаете сложный процент. Есть готовые программки, которые называются калькуляторами сложных процентов (целая куча в сети), а можно попросту забить нужные формулы в таблицу Excel, что я и сделал, специально для этой статьи.
Скачать калькулятор для расчета простых и сложных процентов в Exсel можно здесь. В этом файле я сравнил начисление простых и сложных процентов, при стартовом депо 1000$ и ежемесячной прибыли в 5%. Вот график за 24 месяца, дальше делать не стал, т.к. итак все понятно.
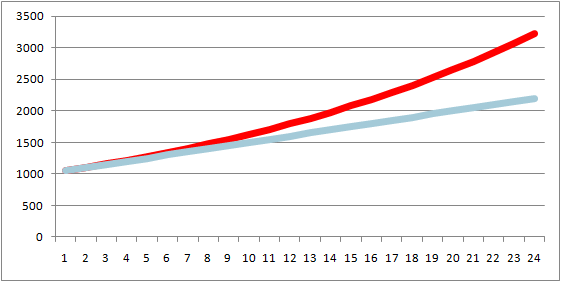
Подсчитывая возможные прибыли, можно заметить, что при увеличении первоначальной суммы вклада, прибыль, получаемая с использованием сложного процента будет существенно увеличиваться. Но пусть это не вводит вас в заблуждение, поскольку это всего лишь теоретический расчет, без учета подводных инвестиционных камней и особенностей каждого инструмента. Если есть какие-нибудь вопросы пишите в комментариях, послезавтра подведу итог очередной ленивой инвестиционной недели.
Всем профита!
Арифметика прибыли
Итак, вы решили приумножить свои сбережения путем вложения их на банковский депозит. Безусловно, банковские служащие постараются дать вам развернутую информацию по всем существующим депозитным предложениям, но зная такой простой арифметический нюанс, как формула сложных процентов, вы легко сможете сами сориентироваться, какой из них подходит наилучшим образом. Есть два варианта проведения расчетов:
Первый вариант расчета подходит для многолетних вкладов.
Здесь в теле формулы учитывается количество лет, на которые рассчитана депозитная программа. Определение и суть этого показателя заключается в том, что в конце оговоренного в депозитном договоре периода полученная прибыль прибавляется к первоначальной сумме вклада, далее этот базис можно использовать для последующей капитализации (что такое капитализация процентов). Для большей наглядности воспользуемся примером расчетов. Допустим, вы собираетесь положить на депозит 100 000,00 рублей, банк предлагает процентную годовую ставку капитализации – 11% а срок договора – 10 лет.
Дадим развернутой пояснение к формуле:
- S – итоговая сумма, которую по условиям договора, вкладчик получает в конце срока. Состоит она из суммы вложенных денег и суммарной величины процентов, начисленных за весь период;
- Р – изначально вложенная сумма денежных средств;
- n – в данном случае обозначает количество лет ( в глобальном смысле подразумевает общее количество капитализирующих операций, проведенных за весь период;
- I – ставка процентов, выставленных банком, за один год пользования деньгами вкладчика.
Вставив в формулу значения, взятые для примера, получим:
Для тех, кого интересует расчет капитализации за короткие временные промежутки, будет лучшим решением воспользоваться следующей формулой:
- К – число дней в расчетном году;
- J – число дней, по прошествии которых, банковское учреждение обязано совершить капитализацию оговоренных процентов.
Расчёты произвести легко, зная все вводные данные. Расчет простых процентов может заинтересовать тех вкладчиков, которые хотели бы снимать проценты помесячно.
Второй вариант расчета сложных процентов
Высчитаем сложный процент, пример второй показывает формулу, где берется месячная ставка капитализации:
n — в данном случае обозначает количество месяцев ( в глобальном смысле подразумевает общее количество капитализирующих операций, проведенных за весь период). Число 12 вводится как еще один указатель расчета помесячно.
Аналогичен расчет и для поквартальной и полугодичной капитализации процентов, лишь с изменением показателей количества капитализирующих операций. Возьмем данные из предыдущего примера, для проведения расчетов с новой формулой:
Отсюда мы видим, что если начисление процентов производится каждый месяц, то вкладчик получает выгоду на 15 000 рублей больше, при условии неприкосновенности начисленных процентов в течении всего срока действия договора. Можно составить график, показывающий наглядно выгоду второго варианта:
Все вышеуказанные примеры показывают, что знание совсем простых арифметических действий дает возможность спланировать собственный доход на несколько лет вперед. Для юридических лиц формулы расчета аналогичны. И если для того чтобы понять, что такое балансовая прибыль, а самое главное рассчитать ее правильно, требуются более глубокие знания и громоздкие формулы, то для определения прямой выгоды от депозитов вполне достаточно базовых расчетов.
Вклад со сложным процентом
Банки предлагают вклад с капитализацией – именно так называется вклад с начислением сложного процента.
Рассматривая расчёт сложных процентов, подразумевается, что к депозиту после каждого периода начисления процентов (так называемый период капитализации) прибавляется полученный доход.
Процент во втором периоде будет начислен на сумму плюс процент за первый период, в третьем периоде расчетная сумма уже увеличится, и процент тоже – он начисляется от суммы, увеличенной в результате прибавления двух разных процентов, причем второй будет выше первого.
Процент начисляется на процент, и каждый последующий период капитализации принесет доход выше, чем он был в прошлые периоды.
Понятно, что с течением времени доходность будет рассчитываться с суммы, заметно превышающей первоначальный депозит.
Длительность срока размещения денег при использования вклада с расчетом накоплений по формуле сложных процентов по вкладу играет ключевую роль. Чем дольше лежат деньги, тем выгоднее вклад.
Хитрость в том, что в линейке банковских вкладов вклады с капитализацией всегда предлагаются под более низкий процент, чем другие срочные вклады.
Для определения, какое вложение выгоднее, рассчитывайте свой доход по формуле.
Кредит со сложным процентом
Особенно важно не попасть в ситуацию, когда процент по кредиту оказывается гораздо выше, чем вы себе представляли.
Это может произойти, если вы не учитываете сложный процент. Рост задолженности становится проблемой, если вы не гасите такой кредит быстро.
Процент, начисленный на увеличенную сумму, растет в соответствии с законами математики. Так же, как и в случае с вкладами, конечная сумма увеличивается с каждым сроком, за который начисляется процент, неравномерно.
Как правило, процент за пользование кредитом берется каждый месяц.
Рассчитать рост задолженности можно по такой же формуле, как и рост вклада при депозите с капитализацией.
Формула расчета сложных процентов
Договоримся обозначать величины так.
Д – начальная сумма, вложенная в банк, или взятая в кредит
С – конечная сумма
п- количество периодов начисления процентов. Таким периодом быть год, квартал, месяц — в соответствии с договором.
X- процентная ставка, за период начисления процентов. Не ставка за год, а именно за тот период, за какой происходит начисление процентов. Например, в договоре указано 12% годовых, а капитализация происходит каждый месяц. Значит, Х в нашем случае равно 1.
Значит, учитывая начисление процентов, мы имеем в конце
- первого месяца С= Д+Д*X/100,
- второго С= Д+Д*X/100+( (Д+Д*X/100)*X/100),
- третьего С=Д+Д*X/100+( (Д+Д*X/100)*X/100)+( Д+Д*X/100+ (Д+Д*X/100)*X/100)*Х/100
Таким образом, проведя математические преобразования, формулу сложных процентов по кредиту можно представить в общем случае как
С= Д*(1+ X/100)n
Видим, что временная составляющая – количество периодов начисления процентов, является степенью. Это говорит о том, что с течением времени конечная сумма С будет расти все более высокими темпами.
Можно рассчитать, как увеличится вклад при депозите сто тысяч под шесть процентов годовых с ежегодной капитализацией на разный срок.
Подставляем в формулу значения для 3 лет, это
100000*(1+0,06)3 =119101,6 рублей, и для 10 лет:
100000*(1+0,06)10 =179084,74
Заметно, что в первые годы вклад рос незначительно, среднегодовой доход за первые три года составил 6366,66 рублей.
Если разделить сумму дохода, полученную после 10 лет накопления, то получим большую ежегодную сумму — 7908 рублей.
Чем больше срок размещения депозита, тем более заметной будет разница.
Еще один интересный расчет – какова разница результата, если рассчитывать итоговую сумму по правилу простого процента в этом же примере? Получаем такие данные:
- Три года – 100000+(100000/100*6)*3= 118000 рублей.
- Десять лет — 100000+(100000/100*6)*10 = 160000 рублей.
Можно сделать вывод, что при одной и той же базовой процентной ставке депозит под сложный процент выгоднее, кредит затратнее.
И прослеживается большая зависимость от срока размещения.
Чем он больше, тем заметнее разница по сравнению с простым процентом.
В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала — выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.
За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) — о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f x , слева от строки ввода значений и адресов ячеек.
В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.
Составляющим формулы расчета будущей стоимости FV = PV(1+r)n в Excel соответствуют следующие функции:
| Общее название | Функция в Excel | Краткое описание |
|---|---|---|
| FV (Future Value) | БС (Будущая Стоимость) | Будущая сумма вклада |
| PV (Present Value) | ПС (Текущая Стоимость) | Текущая стоимость вклада |
| n | КПЕР (Количество Периодов) | Число периодов начисления процентов по вкладу |
| r | СТАВКА | Процентная ставка по вкладу |
Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.
Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет — у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком «минус», т.к. мы эти деньги отдаем, а не получаем.
Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:
- если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим «0» или оставляем поле пустым;
- если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим «1».
В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном — 20 (4 кв. х 5 лет).
А теперь: внимание — вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем «ОК».
Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда — вывод. Проценты по вашему вкладу должны:
- капитализироваться;
- капитализироваться ежемесячно.
Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.
Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!
А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.
Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать — это подумать о завтра сегодня.
Что еще почитать на эту тему?
Как составить инвестиционный план
Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои практикумы и подписаться на рассылку моих торговых сделок.
Оксана Гафаити,автор MindSpace.ru и Trades.MindSpace.ruПонравился? пост? Оставьте свой комментарий ниже?.Получайте мои идеи по рынку в Telegram?: @Mindspace_ru
Что нужно знать при расчете процентов по вкладам (депозитам)
Рано или поздно перед нами встает вопрос о расчете процентов по банковским вкладам (депозитам).
В банковском деле существует два способа начисления процентов:
- по формуле простых процентов;
- по формуле сложных процентов.
Расчет процентов по формулам может совершаться с использованием плавающей и фиксированной процентной ставки.
Фиксированная ставка — процентная ставка, которая остается постоянной на весь срок размещения вклада. Как правило, ставка может быть изменена в момент пролонгации (продления) договора, выплате процентов при досрочном расторжении договора.
Плавающая ставка — процентная ставка, которая может меняться во время размещения вклада. Условия и порядок изменения ставки оговариваются в договоре (например, такими условиями могут быть изменение ставки рефинансирования, изменение курсов валют и т.п.).
Для того, чтобы начать расчет, нам необходимо знать следующие параметры депозита:
- сумма вклада;
- годовая процентная ставка;
- период начисления процентов по депозиту;
- срок размещения депозиа;
- вид процентной ставки — фиксированная или плавающая.
Ежемесячные платежи: принцип формирования
Прежде чем обращаться в тот или иной банк, мы тщательно знакомимся с их кредитными предложениями. На их основе можно попробовать самостоятельно произвести расчет по процентам и высчитать сумму переплаты по нему. Ситуация на кредитном рынке складывается таким образом, что платежи по кредитам необходимо вносить аннуитетным способом — сумма ежемесячного платежа остается неизменной на всем сроке кредитования.
Регулярный платеж формируется обычно из суммы внесения оплаты основного долга и начисленных на нее процентов. Иногда сюда входит оплата дополнительных ежемесячных услуг:
- страховки,
- комиссионного сбора.
В сумме первых выплат основную часть занимают проценты, и только по истечении определенного срока они начинают уменьшаться. Вследствие чего увеличивается сумма, идущая на гашение основного долга.
Практика показывает, что во всех банках кредитные договора формируются с учетом сложных и простых процентов. Простые проценты определяются на базе первоначальной суммы кредита, без зависимости от количества платежей и срока кредитования.
Как посчитать проценты от числа: Высчитать и рассчитать проценты по кредиту — Формула сложных процентов
Сложные проценты по кредиту рассчитываются следующим способом: расчет производится на первоначальную сумму займа, а также на увеличение долга по кредитным обязательствам, который начисляется сразу же после первоначального начисления процентов по кредиту. Поэтому получается, что база для начисления сложных процентов будет постепенно расти, в зависимости от периода начислений.
Проще говоря, расчет таких процентов происходит за счет начисления процентов на проценты. Такая схема выплат по кредитным обязательствам приводит к тому, что к сумме общего долга в каждом последующем месяце плюсуется платеж процентов, а в следующем за основу берется увеличенная сумма первоначального займа.
Примеры вычислений
Формула сложных процентов по кредитным обязательствам выглядит следующим образом:
Условные обозначения:
- T — количество периодических выплат;
- СК — сумма займа по кредиту кредита;
- ПС — процентная ставка, начисляемая на долг за период;
- ЕПn — размер выплаты за n — й период (n принимает значения от 1 до T);
- ПСК – сумма процентов, выплаченных по кредитным обязательствам за весь период.
Как уже говорилось выше, погашение кредита происходит аннуитетными платежами, поэтому:
ЕПn = СК*ПС / (1 — 1 / (1+ПС)^T) – все платежи между собой равны, так как не зависят от n.
ПСК = ЕП*T — СК
Знак ‘^’ в формулах означает возведение в степень.
Рассмотрим пример расчета ежемесячной выплаты:
T = 6 мес.; КС = 9 000 рублей; ПС = 15% годовых/ 12 мес. = 0.0125 ЕП = 9000 * 0.0125 / (1 — 1/ (1.0125)^6) = 112.5 / 0.071825 = 1566.30 рублей ПСК = 1566.30*6 — 9 000 = 397.8 рублей
Пример расчёта общей суммы займа:
Т = 6 мес.; ЕП = 10 000 рублей; СК = 15% годовых/ 12 мес. = 0.0125 СК = 10000 * 0.071825 / 0.0125 = 57460 рублей
Если вам выдали кредит, предусматривающий гашение дифференцированными платежами (основная сумма займа выплачивается равными долями, начисляемые проценты с каждым разом снижаются, как следствие понижается общая сумма платежа), то формула сложных процентов будет рассчитываться следующим образом
ПСК = СК*ПС *(Т + 1) / 2
ЕПn = СК / T + СК*(T-n+1)*ПС / Т
На примере это выглядит так:
Т = 12 мес.; СК = 9 000 рублей; ПС = 15% годовых/ 12 мес. = 0.0125 ПСК = 9000*0.0125*(12+1)/2 = 393,75 рублей ЕП1 = 9000/12 + 9000*12*0.0125/12 = 862,5 рублей … ЕП6 = 9000/12 + 9000*1*0.0125/12 = 759,38 рублей
Формула дохода
Знать хитрости начисления процентов по вкладам не только интересно, ни и весьма полезно, поскольку, решая, где разместить свои деньги, вы можете точно узнать, сколько получите через год, а сколько через два. Управление своими финансами строится на прогнозировании прибылей и убытков, и лучше заранее просчитать перспективы вклада, чем впоследствии обмануться в своих ожиданиях.
Специалисты банков, начисляя доход по вкладам граждан, пользуются двумя методиками расчетов. Они используют формулы простых и сложных процентов. Проценты по этим формулам считаются с применением плавающей или фиксированной ставки. Разберемся, что это такое.
- Фиксированная ставка – это процентная ставка, прописанная в договоре об открытии депозита. Она остается неизменной до конца договора, то есть фиксируется. Поменяться ставка может только при продлении срока договора на новый срок. Банк может изменить размер фиксированной процентной ставки в случае досрочного прекращения действия договора при форме вклада «до востребования» , при начислении процентов за фактически прошедшее время действия вклада.
- Плавающая ставка – это процентная ставка, которая на протяжении срока депозита может менять свое значение. Характер изменения плавающей ставки отражается в заключаемом с вкладчиком договоре. Почему плавает ставка? Это может происходить из-за изменения ставки рефинансирования, валютных курсов. Когда вклад переводится в другую функциональную категорию, процентная ставка может поменяться.
Чтобы правильно рассчитать проценты по вкладу, нужно иметь следующие данные:
- Размер суммы вклада;
- Величину процентной ставки по типу вклада;
- Динамику начисления дохода — ежедневно, ежемесячно и т.д.;
- Срок действия договора вклада;
- Вид применяемой ставки – фиксированная или плавающая.
Настало время заняться непосредственно формулами. Давайте познакомимся с ними поближе.
Формула простых процентов
Простые проценты начисляются банком в случае, когда выплата дохода следует в конце срока вклада, проценты могут переводиться на отдельный счет, таким образом, формуларасчета простых процентов применима к сберегательным вкладам и не предполагает капитализации процентов.
Собираясь открыть вклад, обращайте внимание на то, какие проценты будут начислены – простые или сложные. Если сумма на вкладе приличная, срок большой, а банк предлагает простые проценты, это значит, что сумма дохода заведомо будет банком занижена и вам это не выгодно. Формула расчета простых процентов:
В этой формуле:
- S — деньги для возврата клиенту в конце срока депозита. Это первоначальная сумма вклада плюс проценты;
- I – значение ставки % годовых;
- t – количество дней начисления процентов;
- K – дни в календарном году — 365 или 366;
- P – изначальная сумма денег на вкладе;
- Sp – проценты, то есть доход вкладчика.
Формула сложных процентов
Формула сложных процентов применятся в отношении вкладов, по которым предусмотрена капитализация, а проценты начисляются ежемесячно, ежеквартально, то есть регулярно через одинаковые промежутки времени. Проценты увеличивают сумму вклада, таким образом, проценты начисляются на проценты.
Банки в своем большинстве предпочитают поквартальное начисление сложных процентов. Есть некоторые кредитные организации, у которых капитализация происходит в конце срока депозита, такой фокус представляет собой рекламное ухищрение и не является сложными процентами, поскольку, формула, по которой банкиры их считают, это формула простых процентов. Цель – подтолкнуть клиента к продлению срока договора.
Рассмотрим формулу сложных процентов:
Что означают символы:
- I – значение ставки % годовых;
- j – количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;
- K – дни в календарном году — 365 или 366;
- P – изначальная сумма денег на вкладе;
- n — количество операций по капитализации начисленных процентов в течение общего срока привлечения денежных средств;
- S — деньги для возврата клиенту в конце срока депозита. Это первоначальная сумма вклада плюс проценты.
Когда начисляются проценты, следует обратить внимание на одну деталь. При подсчете количества дней во время срока хранения денег, банки не учитывают день прекращения вклада.
Приведенные нами формулы помогут вам самостоятельно рассчитать свои ожидаемые доходы и
позволит весьма точно прогнозировать свои доходы по планируемому вкладу.
Автор Аргунов Дмитрий Борисович
«); up.type = ‘text/javascript’; up.async = true; up.src = «//w.uptolike.com/widgets/v1/widgets.js?b=fb.tw.vk.gp&id=1246405&o=1&m=1&sf=2&ss=1&sst=1&c1=ededed&c1a=0.0&c3=ff9300&c5=ffffff&mc=1&c2=000000&c4=ffffff&c4a=1.0&mcs=0&sel=1&fol=0&sel=1&scs=24&he=0&c=» + cmp + «&url=»+encodeURIComponent(url); s.parentNode.insertBefore(up, s); })(document,»__uptlk»); /* uptolike share end */
Вклады с простым процентом
Простой способ начисления процентов – это когда начисление процентов осуществляется один раз в конце срока вклада. В банковских договорах процентная ставка указывается за год. Для других периодов времени нужно срок вклада перевести в дни. Простые проценты считаются по такой формуле:
|
В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Td – срок вклада в днях, Ty– количество дней в году. |
Пример 1. Вы положили 20 000 рублей на полтора года под простой процент с годовой ставкой 8%.
20 000 * (1 + 0,08 * (548 / 365)) = 22 402,20
Вклады со сложным процентом
Сложные проценты – это проценты, начисленные не только с первоначальной величины депозита, но и с процентов, полученных за предыдущие сроки. Процесс прибавления процентов к первоначальной величине вклада называется капитализацией процентов. Она обычно бывает ежегодная, ежеквартальная, ежемесячная. Каждый период начисленные проценты не снимаются, а прибавляются к имеющейся величине вклада и уже сами начинают принимать участие в образовании новой прибыли. Только в таком случае сложный процент начинает работать. Расчёт сложных процентов производится по следующей формуле:
В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Ny– количество периодов капитализации в году, Nd – количество периодов капитализации за весь период вклада. |
Наращение по простым процентам
В общем случае наращение по годовой ставке простых процентов вычисляют по формуле:
FV = PV (1 + r * n)
где FV— будущая стоимость (величина); PV — современная величина; n — число периодов (лет); r — процентная ставка.
На практике продолжительность краткосрочной операции обычно меньше года. В этом случае срок проведения операции корректируется следующим образом:
ЕЩЕ СМОТРИТЕ: Производственный леверидж и его влияние на прибыль
где t — число дней проведения операции; В — временная база (число дней в году: 360, 365 или 366).
С учетом корректировки срока операции ее будущую стоимость можно определить как:
FV = PV (1 + r * [t /B]).
Обычно при определении продолжительности операции даты ее начала и окончания считаются за один день.
В процессе проведения анализа в качестве временной базы часто удобно использовать условный, или финансовый, год, состоящий из 360 дней (12 месяцев по 30 дней). Исчисляемые по такой базе проценты называют обыкновенными, или коммерческими.
Точные проценты получают при базе, равной фактическому числу дней в году, т. е. при В = 365 или 366.
Пример. Покупатель предоставил коммерческий кредит под гарантию оплаты продукции на сумму 10 000 ед. через 30 дней. Ставка по кредиту определена в размере 30% годовых. Какова будет сумма оплаты по контракту?
Вычислим ее:
а) с использованием обыкновенных процентов
FV = 10 000 * (1 + 0,30 * (30 / 360)) = 10 250 ед.;
б) с использованием точных процентов
FV= 10 000 * (1 + 0,30 * (30 / 365)) = 10 246,58 ед.
В свою очередь, срок продолжительности операции также может быть приблизительным (когда месяц принимается равным 30 дням) или точным (фактическое число дней в каждом месяце).
Таким образом, в зависимости от параметров t и В возможны следующие варианты начислений процентов:
- 365/365 — точное число дней проведения операции и фактическое число дней в году;
- 365/360 — точное число дней проведения операции и финансовый год (12 месяцев по 30 дней);
- 360/360 — приближенное число дней проведения операции (месяц принимается равным 30 дням) и финансовый год (12 месяцев по 30 дней).
Обыкновенные проценты (360/360) более удобно использовать в аналитических расчетах. Этим объясняется популярность их применения на практике в большинстве развитых стран, включая США и государства Европы.
В России в основном применяются точные проценты (365/365). В частности, они используются в официальных методиках Центрального банка РФ и Минфина России для расчета доходности по краткосрочным государственным обязательствам.
Дисконтирование по сложным процентам
Формулу для определения современной величины по сложным процентам можно легко вывести формулы сложных процентов делением его обеих частей на величину (1 + r) n. Выполнив соответствующие математические преобразования, получим:
PVn = FVn / (1 + r)n
Пример. Выплаченная по 3-летнему депозиту сумма составила величину 100 ед. Определить первоначальную величину вклада, если ставка по депозиту равна 8% годовых. Аналитическое решение задачи будет иметь следующий вид:
PV = 100,00 / (1 + 0,08)3 = 79,38 ед.
Если начисление процентов осуществляется m раз в году, соотношение будет иметь вид:
PV n, m = FVn (1 + r / m)mn
Методы наращения и дисконтирования играют важную роль в финансовом менеджменте, так как являются инструментарием для оценки потоков платежей.
Изучите простые и сложные проценты в практическом курсе «Финансовый менеджмент: управление финансами»:

Изучите сегодня
Также смотрите
Как начисляются проценты по вкладам
На самом деле здесь процесс начисления достаточно простой. Банк указывает клиенту годовую ставку, например, 8% и на всю сумму инвестиции ее начисляет. Приведем простой пример: сумма вклада 10000 рублей, ставка 8%, срок 1 год. По окончании месяца сумма к выдаче составит 10800 рублей. В данном примере применялась формула простых процентов, которая выглядит так:
S=D*(P/100), где:
- S – итоговая сумма, по окончании срока действия договора;
- D – сумма инвестиций;
- P – годовой процент.
Что касается индивидуальных условий банковского обслуживания, то всё зависит от внутреннего регламента коммерческой организации. То есть, некоторые банки начисляют доход по окончании срока действия договора, другие кредитно-финансовые организации рассчитывают доход с определенной периодичностью, например, один раз в месяц, квартал или полугодие. Соответственно, клиент может получать свое вознаграждение на протяжении срока действия договора.
Кроме всего прочего, в банковской терминологии применяются такие понятия, как фиксированный и плавающий годовой процент. Фиксированное значение — это то, которое действует от начала до конца срока вложений и может измениться только при том обстоятельстве, если предусмотрена автоматическая пролонгация договора. По той причине, что в данном случае банк устанавливает тот процент, который действует на дату пролонгации.
Плавающий процент применяется при депозитах с возможностью пополнения счёта. Например, по условия банковского вклада владелец депозитного счёта может пополнять его на определенную сумму, при этом годовой процент полностью зависит от размера вклада, а постольку, поскольку он пополняемый, то за весь период срока действия договора сумма увеличивается, соответственно, вместе с ней увеличивается и годовой процент.
Посчитать проценты за месяц достаточно просто, нужно применить формулу, указанную выше, но с небольшой корректировкой: S=D*(P/100/12), то есть вклад с вышеуказанными параметрами принесет своему владельцу доход в размере 67 рублей.
Обратите внимание, что расчеты по представленной формуле предварительные, потому что банк рассчитывает прибыль для вкладчиков за каждый день, а затем умножает на количество дней в периоде.
Капитализация процентов
На самом деле вклады под сложные проценты принято называть вклад с капитализацией процентов. Что это такое? Если говорить просто, то для вкладчика это означает начисление процентов на проценты. Например, по условиям банковского вклада прибыль от депозита начисляется ежемесячно, но, постольку, поскольку она остается не востребована вкладчиком, ее банк прибавляет к телу депозита.
Здесь размер прибыли во многом зависит от количества периодов капитализации. Многие крупные банки, в частности, Сбербанк России, ВТБ 24 и другие, предлагают своим клиентам капитализацию один раз в квартал, то есть каждые 3 месяца. А другие коммерческие банки могут вовсе рассчитывать прибыль один раз в год, соответственно, первая капитализация будет только через 12 месяцев, а именно на этот срок большинство заключает договор.
Вернемся к вопросу, как выглядит формула сложных процентов для банковских вкладов. Попробуем рассчитать прибыль от депозита за один год:
S=D?(1+N?L100?365)^x, где:
- S – общая сумма денежных средств, подлежащая возврату вкладчику по истечении срока действия депозитного договора;
- N – годовой процент без учета капитализации;
- L – число дней в том периоде, за который банк проводит капитализацию процентов;
- x – количество капитализаций за весь период действия договора;
- D – сумма инвестиций в банковский вклад.
Попробуем по данной формуле рассчитать депозит со следующими параметрами:
- сумма инвестиций — 10000 рублей;
- капитализация осуществляется один раз в месяц (всего в году 365 дней), соответственно здесь L будет равно 365/12=30,41;
- количество капитализации — 12;
- годовая ставка — 8%;
Теперь произведем расчет:
S=10000?(1+8?30,41100?365)^12= 10830 рублей – это общая прибыль по депозиту на конец срока действия договора.
Как видно, посчитать самостоятельно прибыль от депозита не так сложно. Но банки рассчитывают доход вкладчика с учетом капитализации процентов несколько по-другому. То есть, от базовой процентной ставки высчитывается эффективный процент по вкладу, то есть тот который будет действовать с учетом причисления процентов к телу депозита на протяжении срока действия депозитного договора.
Формула сложных процентов по вкладам будет выглядеть следующим образом:
((1+P/12)^x-1)?12/x, где:
- P – это годовой процент без учета капитализации;
- x – количество периодов капитализации (при том условии, если она осуществляется ежемесячно).
Рассмотрим простотой пример расчета процентной ставки, при том условии, что базовое значение 8% в год. Расчет сложной ставки:
((1+8/100/12)^ 12-1)?12/12=0,083.
То есть, согласно данным расчетам базовая ставка 8% будет увеличена на 0,083% при капитализации процентов. Если же капитализация будет осуществляться один раз в квартал, то рассчитать эффективную ставку можно по следующей формуле:
((1+P/100/4)^4-1)?100%.
Считаем вклад с теми же параметрами ((1+8/100/4)^4-1)?100%=0,2682417945625, или приблизительно 0,268.
Обратите внимание, что информация по расчетам носит справочный характер, окончательное значение по вашему договору вы можете узнать непосредственно в банке.
Расчет прибыли для вклада с пополнением
Большинство вкладчиков сегодня выбирают депозитные программы с возможностью пополнения. Суть данного предложения заключается в том, что за весь период действия договора клиент может пополнять свой счет на определенную сумму. Несомненно, в данном случае прибыль будет рассчитываться совершенно по-другому.
Кстати, рассчитать прибыль по депозиту можно без сложных формул. Приведем простой, рассмотрим депозит с ежемесячным пополнением и капитализацией. Для этого возьмем следующие данные:
- сумма 10000 рублей;
- ставка с учетом капитализации – 8,083%;
- срок 3 месяца;
- капитализация ежемесячно;
- ежемесячное пополнение 1000 рублей.
Считаем прибыль:
- 1 месяц – 10000+(10000?8,083/100/12)+1000=11067,358 рублей;
- 2 месяц – 11067,358+(11067,358?8,083/100/12)+1000=12141,905 рублей;
- 3 месяц – 12141,905+(12141,905?8,083/100/12)+1000=13223,690 рублей.
Таким образом, по истечении срока действия договора сумма инвестиций составит 13 тысяч рублей. Чистая прибыль будет равняться 223,69 рублям.















